The intuitive notion of a “space” has seen a variety of incarnations in mathematics, in fields ranging from topology to geometry in all its flavours.
The subject of Non-Commutative Algebraic Geometry (NCAG) pushes the boundaries of the concept of space by using algebraic and categorical models in contexts where classical point-set based representations fail.
This summer school is aimed at gaining understanding of key concepts and examples that motivate NCAG and which see their application in Homological Mirror Symmetry (HMS), which has its origins in mathematical physics.
The programme provides two parallel courses, one on Algebraic Models for Spaces (AMS) and one on HMS, which consist each of lectures by experts in the field and highly interactive problem sessions in groups tailored to a shared background knowledge.
- In the AMS course, we furnish the background to model non-commutative spaces, working towards A-infinity algebras and quasi-categories as models for infinity-categories.
- In the HMS course, we illustrate the idea of NCAG by Mirror Symmetry (MS) by starting from Classical Mirror Symmetry as an exchange of numerical data between “mirror” complex and symplectic space. From there, we build towards Kontsevich’ HMS conjecture.
The programme also includes one or two afternoons of research talks by experts in the field.
Prerequisites
Familiarity with the following “basic” prerequisites in category theory (CT), algebraic topology (AT) and algebraic geometry (AG) is expected for everyone taking part in the course:
- category theory language (CT)
- tensor products and chain complexes (AT),
- homotopy of spaces (AT),
- algebraic varieties (AG)
As the interactive problem sessions will be held in smaller groups at different paces, understanding of the following “advanced” topics is valuable:
(co)limits, adjunctions (CT)
simplicial sets (AT)
homotopy theory (AT)
schemes and sheaf cohomology (AG)
A concrete list of prerequisites with sources and references is available here.
Day to day programme
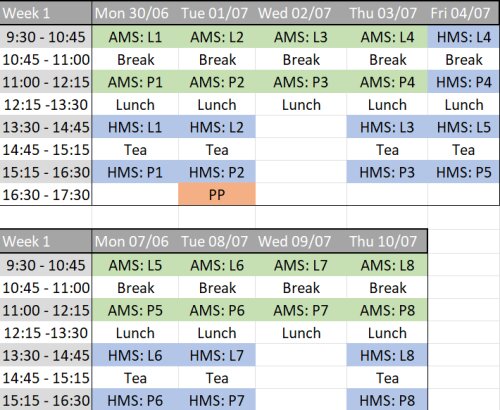
Below you can find the schedule for the summer school. The AMS course is highlighted in green and the HMS course is highlighted in blue. Lectures are indicated by Ln and practice sessions by Pn. On Tuesday of the first week, there is time for short presentations given by the participants, highlighted in orange and indicated by PP.
Target group
The summer school is designed for both recent Master students and beginning PhD students with a background in Mathematics or Mathematical physics who have an active interest in algebra and geometry.
Prerequisites
Familiarity with the following “basic” prerequisites in category theory (CT), algebraic topology (AT) and algebraic geometry (AG) is expected for everyone taking part in the course:
- category theory language (CT)
- tensor products and chain complexes (AT),
- homotopy of spaces (AT),
- algebraic varieties (AG)
As the interactive problem sessions will be held in smaller groups at different paces, understanding of the following “advanced” topics is valuable:
- (co)limits, adjunctions (CT)
- simplicial sets (AT)
homotopy theory (AT)
schemes and sheaf cohomology (AG)
Campus
This summer school takes place at Middelheim Campus of the University of Antwerp. This campus can be reached from the city centre by bike or public transport.
However, please check the travel info and the distance before booking accomodation.
Micro-credential and study credits (ECTS)
Successful completion of the summer school can be awarded with 3 credits according to the European Credit Transfer System (ECTS). Credits will be awarded by the University of Antwerp on the base of 100 % (active) participation during the course, group work and submission of exercises and a written summary on some part of the lectures. To include the credits in the curriculum at the home institution, participants need an agreement with the responsible person at their university. A certificate will be awarded at the end of the programme. All certificates of completion are issued as a micro-credential.
Students of the University of Antwerp who wish to include the ECTS credits earned during an Antwerp Summer or Winter University programme as part of their study programme must register via Mobility Online and SisA.
Learning outcomes
- The student has gained an understanding of the state of the art of two cutting-edge research fields: algebraic models for spaces and homological mirror symmetry.
- The student is familiar with a wide variety of new concepts and results, such as A-infinity algebras and how they play a part in homological mirror symmetry.
- The student understands how key ideas from algebraic topology, algebraic geometry and symplectic geometry shape the concept of a “noncommutative space”.
- The student is able to perform the first calculation of the various relevant cohomology groups and interpret the results.
- The student can apply the concepts of the course in examples.